Theory
State Oriented Programming is a way of thinking about programming not as process flow but as state and behaviour. With traditional programming, and by traditional I include procedural, functional and OO programming styles, the code will contain conditional statements, usually in the form of ‘if’ statements, with possibly, case/switch statements, but it will almost certainly contain some form of logic to decide whether an action should be performed or not. The purpose of the conditional code will be varied, but it would be a strange program that did not contain any conditional statements.
However, if we analyze these Conditional Statements what they are actually saying is ‘If object/code is in this state, then do ‘X’ if not then do ‘Y’.
State Oriented Programming tries (and I will come on to the ‘tries’ in a moment) to change that narrative by replacing the conditional statements with a call to a function, where the function that will be called is determined ahead of time, whenever the state of the program/object changes.
So, instead of the ‘If-Then-Else’ clause (or something similar) , we have ‘Execute_Function_X()’, where the function ‘X’ being executed has changed to match the object state.
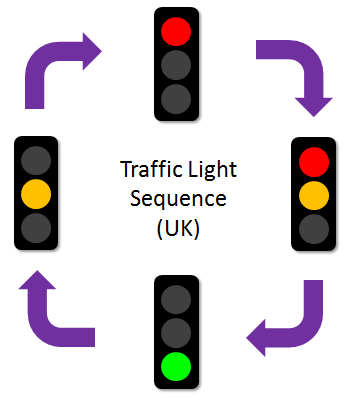
As an example, consider modelling UK traffic lights:
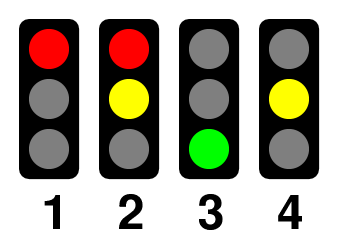
A traditional C# code block might look like the following:
namespace TrafficLight
{
public enum Switch { Off, On }
public enum Signal { Stop = 0, ReadyGo, Go, ReadyStop };
public class ClassicTrafficLight
{
private Signal currentSignal;
public ClassicTrafficLight()
{
// Start with Red On.
SwitchRed(Switch.On);
currentSignal = Signal.Stop;
}
/*
* Change Traffic Light from current state to next state
*/
public void ChangeSignal(Signal currentSignal)
{
switch (currentSignal)
{
case Signal.Stop:
SwitchAmber(Switch.On);
currentSignal = Signal.ReadyGo;
break;
case Signal.ReadyGo:
SwitchRed(Switch.Off);
SwitchAmber(Switch.Off);
SwitchGreen(on);
currentSignal = Signal.Go;
break;
case Signal.Go:
SwitchGreen(Switch.Off);
SwitchAmber(Switch.On);
currentSignal = Signal.ReadyStop;
break;
case Signal.ReadyStop:
SwitchAmber(Switch.Off);
SwitchRed(Switch.On);
currentSignal = Signal.Stop;
break;
default:
throw new Exception("Unknown signal state");
}
}
}
}Using an SOP approach the above might be replaced by:
using System;
namespace SOPTrafficLight
{
public enum Switch { Off, On }
public enum Signal { Stop = 0, ReadyGo, Go, ReadyStop };
public class SOPTrafficLight
{
private Func<Signal>[] signalChanges;
private Signal currentSignal;
public SOPTrafficLight()
{
signalChanges =
new Func<Signal>[] { Stop, ReadyGo, Go, ReadyStop };
currentSignal = Signal.Stop;
SwitchRed(Switch.On);
}
public void ChangeSignal()
{
currentSignal = signalChanges[(int)currentSignal]();
}
private Signal Stop()
{
SwitchAmber(Switch.On);
return Signal.ReadyGo;
}
private Signal ReadyGo()
{
SwitchRed(Switch.Off);
SwitchAmber(Switch.Off);
SwitchGreen(on);
return Signal.Go;
}
private Signal Go()
{
SwitchGreen(Switch.Off);
SwitchAmber(Switch.On);
return Signal.ReadyStop;
}
private Signal ReadyStop()
{
SwitchAmber(Switch.Off);
SwitchRed(Switch.On);
return Signal.Stop;
}
}
}
First thing to notice: Examine the ChangeSignal method. With S.O.P. it is a one line method, and the whole code contains no conditional statements. No ‘IF‘s, no ‘Switch/Case‘, no conditional statements at all!!! How cool is that.
OK – so I hear you say that all I have done is encapsulate the code in the case clauses within functions. On the actual lines of functioning code that is (possibly) a valid viewpoint. But did you even think you could model a set of trafiic lights without conditional statements. Be honest, you didn’t did you.
What we have done is to tie functions to state. Every state change of the traffic light is encapsulated in a state change function. It is triggered in isolation from every other possible state, and, the most important point, the function that will be executed next is detemined ahead of it being executed.
There is no code that is saying “if in this state, then do this”. The state that the traffic light is in dictates the action it will take, and that action is pre-determined.
Now the traffic light scenario has a limited number of states and state transitoins. Increase the numbers of states and transitions, I would argue that an S.O.P. approach very quickly produces code that is easier to maintain, understand, and, crucially, Test.
As an aside, Note: Any switch statement can be replaced by a vector of functions, and your code will be better for doing so.
More Complex State Maps, More reason for S.O.P.
The traffic light above is an example of a simple sequential state changing object. The traffic light only ever executes the one line in the ChangeState function. All we instruct the object to do is move from its current state to the next state.
However objects’ states are rarely this simple, More often than not an object will have a matrix of states. So lets examine a more complex example: A Calculator.
Calculator
I have chosen a calculator because:
- It is something familiar to us all
- It is self contained.
- We can start with a limited functionality and then expand on that.
For the initial implementation I am restricting the functionality to accepting the following inputs:

- Numerics: (Numbers 0-9)
- Fraction indicator: (.)
- Binary operators: (+, -, /, *)
- Result Operator (=)
- Clear accumulator (I know – the above image is missing a ‘Clear’ button, lets assume it is on the side.)
Even with this limited set of inputs we already have a number of state issues to contend with:
- The Fraction indicator (decimal point) is only valid in certain circumstances.
- The Fraction indicator (decimal pont) determines the effective value of the next numeric input.
- A Binary Operator cannot follow a Binary Operator.
- The Result operator cannot follow a Binary Operator.
- The earliest the execution of Binary Operator can take place is when input of the second operand has been completed.
- A Numeric input following a completed calculation means start a new calculation, whilst a Binary Operator input means take the current result as being the first operand.
Calculator Functionality
The Calculator will have as its initial condition a value = 0.
If the first key pressed at the start of a calculation is an Operator, then the Calculator’s value from its previous calculation (or 0 if this is the first calculation) will be used as the first Operand. If the first key pressed is Numeric, then it will be assumed that a new calculation is being started, with a new initial operand, and any existing value will be disgarded.
Calculator States
If we consider the defining of the operands as being the main focus of the calculation states, and the non numeric keys – Operators, Decimal Point, ‘=’ and Clear as state transition triggers, then we have nine possible states:
- Initial Start up.
- Defining integral numeric of first operand
- Defining decimal part of first operand.
- Defining first integral numeric of second operand
- Defining subsequent integral numberic of second operand.
- Defining decimal part of second operand.
- Calculation Completed
- Reset (Cleared)
- Errored.
Now whilst we have nine possible states, if we condier the initial state equal to a calculated state with a result of zero, and the Reset and Errored states taking us back to the Initial state, then the states numbered 1, 7, 8, and 9 are in effect identical, and that bring us down to six states. (Renumbered 0-5)
- State0: Start of Calculation
- State1: Defining Integral part of first operand
- State2: Defining Decimal part of first operand.
- State3: Defining First Integral of second operand
- State4: Defining Subsequent Integral part of second operand
- State5: Defining Decimal part of second operand
The six states have the following possible state transitions:
- State0
- 0-9 -> State1
- Dec pt -> State1
- Operator -> State3
- Clear or = -> State0
- State1
- 0-9 -> State1
- Dec pt -> State2
- Operator -> State3
- Clear or = -> State0
- State2
- 0-9 -> State2
- Dec Pt -> Error, then State0
- Operator -> State3
- Clear or = -> State0
- State3
- 0-9 -> State4
- Dec Pt -> State5
- Operator -> Error, then State0
- Clear or = -> State0
- State4
- 0-9 -> State4
- Dec pt -> State5
- Operator -> State3
- Clear or = -> State0
- State5
- 0-9 -> State5
- Dec Pt -> Error, then State0
- Operator -> State3
- Clear or = -> State0
Calculator State Actions
I am proposing a very simplistic implementation in which for each of the six states we create a dictionary of Action and TrasnsisionState for each of the seventeen possible keys
- Numeric (0 – 9)
- Decimal point
- Operators (+ – * /)
- Result
- Clear
// Start of Calculation
state0 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(StartOfNewCalculation, States.State1) },
{ '1', new StateAction(StartOfNewCalculation, States.State1) },
{ '2', new StateAction(StartOfNewCalculation, States.State1) },
{ '3', new StateAction(StartOfNewCalculation, States.State1) },
{ '4', new StateAction(StartOfNewCalculation, States.State1) },
{ '5', new StateAction(StartOfNewCalculation, States.State1) },
{ '6', new StateAction(StartOfNewCalculation, States.State1) },
{ '7', new StateAction(StartOfNewCalculation, States.State1) },
{ '8', new StateAction(StartOfNewCalculation, States.State1) },
{ '9', new StateAction(StartOfNewCalculation, States.State1) },
{ '.', new StateAction(StartOfNewCalculation, States.State1) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining integral part of first operand State
state1 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FirstIntegralDigit, States.State1) },
{ '1', new StateAction(FirstIntegralDigit, States.State1) },
{ '2', new StateAction(FirstIntegralDigit, States.State1) },
{ '3', new StateAction(FirstIntegralDigit, States.State1) },
{ '4', new StateAction(FirstIntegralDigit, States.State1) },
{ '5', new StateAction(FirstIntegralDigit, States.State1) },
{ '6', new StateAction(FirstIntegralDigit, States.State1) },
{ '7', new StateAction(FirstIntegralDigit, States.State1) },
{ '8', new StateAction(FirstIntegralDigit, States.State1) },
{ '9', new StateAction(FirstIntegralDigit, States.State1) },
{ '.', new StateAction(DecimalPoint, States.State2) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining decimal part of first operand
state2 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FirstFractionalDigit, States.State2) },
{ '1', new StateAction(FirstFractionalDigit, States.State2) },
{ '2', new StateAction(FirstFractionalDigit, States.State2) },
{ '3', new StateAction(FirstFractionalDigit, States.State2) },
{ '4', new StateAction(FirstFractionalDigit, States.State2) },
{ '5', new StateAction(FirstFractionalDigit, States.State2) },
{ '6', new StateAction(FirstFractionalDigit, States.State2) },
{ '7', new StateAction(FirstFractionalDigit, States.State2) },
{ '8', new StateAction(FirstFractionalDigit, States.State2) },
{ '9', new StateAction(FirstFractionalDigit, States.State2) },
{ '.', new StateAction(DecimalPointNotAllowed, States.State0) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining first integral number of second operand
state3 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(IntegralDigit, States.State4) },
{ '1', new StateAction(IntegralDigit, States.State4) },
{ '2', new StateAction(IntegralDigit, States.State4) },
{ '3', new StateAction(IntegralDigit, States.State4) },
{ '4', new StateAction(IntegralDigit, States.State4) },
{ '5', new StateAction(IntegralDigit, States.State4) },
{ '6', new StateAction(IntegralDigit, States.State4) },
{ '7', new StateAction(IntegralDigit, States.State4) },
{ '8', new StateAction(IntegralDigit, States.State4) },
{ '9', new StateAction(IntegralDigit, States.State4) },
{ '.', new StateAction(DecimalPoint, States.State5) },
{ '+', new StateAction(OperatorNotAllowed, States.State0) },
{ '-', new StateAction(OperatorNotAllowed, States.State0) },
{ '*', new StateAction(OperatorNotAllowed, States.State0) },
{ '/', new StateAction(OperatorNotAllowed, States.State0) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining integral part of second operand
state4 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(IntegralDigit, States.State4) },
{ '1', new StateAction(IntegralDigit, States.State4) },
{ '2', new StateAction(IntegralDigit, States.State4) },
{ '3', new StateAction(IntegralDigit, States.State4) },
{ '4', new StateAction(IntegralDigit, States.State4) },
{ '5', new StateAction(IntegralDigit, States.State4) },
{ '6', new StateAction(IntegralDigit, States.State4) },
{ '7', new StateAction(IntegralDigit, States.State4) },
{ '8', new StateAction(IntegralDigit, States.State4) },
{ '9', new StateAction(IntegralDigit, States.State4) },
{ '.', new StateAction(DecimalPoint, States.State5) },
{ '+', new StateAction(CalcAndOperator, States.State3) },
{ '-', new StateAction(CalcAndOperator, States.State3) },
{ '*', new StateAction(CalcAndOperator, States.State3) },
{ '/', new StateAction(CalcAndOperator, States.State3) },
{ '=', new StateAction(CalcAndResult, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining decimal part of subsequent operand.
state5 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FractionalDigit, States.State5) },
{ '1', new StateAction(FractionalDigit, States.State5) },
{ '2', new StateAction(FractionalDigit, States.State5) },
{ '3', new StateAction(FractionalDigit, States.State5) },
{ '4', new StateAction(FractionalDigit, States.State5) },
{ '5', new StateAction(FractionalDigit, States.State5) },
{ '6', new StateAction(FractionalDigit, States.State5) },
{ '7', new StateAction(FractionalDigit, States.State5) },
{ '8', new StateAction(FractionalDigit, States.State5) },
{ '9', new StateAction(FractionalDigit, States.State5) },
{ '.', new StateAction(DecimalPointNotAllowed, States.State0) },
{ '+', new StateAction(CalcAndOperator, States.State3) },
{ '-', new StateAction(CalcAndOperator, States.State3) },
{ '*', new StateAction(CalcAndOperator, States.State3) },
{ '/', new StateAction(CalcAndOperator, States.State3) },
{ '=', new StateAction(CalcAndResult, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
To enable us to have common operator code, and yet execute specific functions for specific operators we create a dictionary of Operator Functions.
OperatorFunctions = new Dictionary<char, Func<double, double, double>> {
{ '+', PlusOperator},
{ '-', MinusOperator },
{ '*', MultiplicationOperator },
{ '/', DivisionOperator } };Having defined the all state transitions and the actions to perform on the state transitions, the actual code to execute a key press becomes:
public double Calculate(char key)
{
stateSet[state][key].Action(key);
state = stateSet[state][key].TransitionToState;
return accumulator;
}Plus the transition functions – but they are small self-contained code snippets.
Putting the whole thing together, including the functions to execute the operators and the StateAction class we have the following as a fully functioning CalculatorEngine – with NO conditionals
using System;
using System.Collections.Generic;
namespace Calculator.Models
{
public enum States { State0 = 0, State1, State2, State3, State4, State5 };
public class CalculatorEngine
{
private char operatorInWaiting;
private double currentOperand;
private double fractionalDivisor;
private double accumulator;
private States state;
private IDictionary<char, StateAction> state0;
private IDictionary<char, StateAction> state1;
private IDictionary<char, StateAction> state2;
private IDictionary<char, StateAction> state3;
private IDictionary<char, StateAction> state4;
private IDictionary<char, StateAction> state5;
private IDictionary<States, IDictionary<char, StateAction>> stateSet;
private IDictionary<char, Func<double, double, double>> OperatorFunctions;
public CalculatorEngine()
{
// Start of Calculation
state0 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(StartOfNewCalculation, States.State1) },
{ '1', new StateAction(StartOfNewCalculation, States.State1) },
{ '2', new StateAction(StartOfNewCalculation, States.State1) },
{ '3', new StateAction(StartOfNewCalculation, States.State1) },
{ '4', new StateAction(StartOfNewCalculation, States.State1) },
{ '5', new StateAction(StartOfNewCalculation, States.State1) },
{ '6', new StateAction(StartOfNewCalculation, States.State1) },
{ '7', new StateAction(StartOfNewCalculation, States.State1) },
{ '8', new StateAction(StartOfNewCalculation, States.State1) },
{ '9', new StateAction(StartOfNewCalculation, States.State1) },
{ '.', new StateAction(StartOfNewCalculation, States.State1) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining integral part of first operand State
state1 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FirstIntegralDigit, States.State1) },
{ '1', new StateAction(FirstIntegralDigit, States.State1) },
{ '2', new StateAction(FirstIntegralDigit, States.State1) },
{ '3', new StateAction(FirstIntegralDigit, States.State1) },
{ '4', new StateAction(FirstIntegralDigit, States.State1) },
{ '5', new StateAction(FirstIntegralDigit, States.State1) },
{ '6', new StateAction(FirstIntegralDigit, States.State1) },
{ '7', new StateAction(FirstIntegralDigit, States.State1) },
{ '8', new StateAction(FirstIntegralDigit, States.State1) },
{ '9', new StateAction(FirstIntegralDigit, States.State1) },
{ '.', new StateAction(DecimalPoint, States.State2) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining decimal part of first operand
state2 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FirstFractionalDigit, States.State2) },
{ '1', new StateAction(FirstFractionalDigit, States.State2) },
{ '2', new StateAction(FirstFractionalDigit, States.State2) },
{ '3', new StateAction(FirstFractionalDigit, States.State2) },
{ '4', new StateAction(FirstFractionalDigit, States.State2) },
{ '5', new StateAction(FirstFractionalDigit, States.State2) },
{ '6', new StateAction(FirstFractionalDigit, States.State2) },
{ '7', new StateAction(FirstFractionalDigit, States.State2) },
{ '8', new StateAction(FirstFractionalDigit, States.State2) },
{ '9', new StateAction(FirstFractionalDigit, States.State2) },
{ '.', new StateAction(DecimalPointNotAllowed, States.State0) },
{ '+', new StateAction(Operator, States.State3) },
{ '-', new StateAction(Operator, States.State3) },
{ '*', new StateAction(Operator, States.State3) },
{ '/', new StateAction(Operator, States.State3) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining first integral number of second operand
state3 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(IntegralDigit, States.State4) },
{ '1', new StateAction(IntegralDigit, States.State4) },
{ '2', new StateAction(IntegralDigit, States.State4) },
{ '3', new StateAction(IntegralDigit, States.State4) },
{ '4', new StateAction(IntegralDigit, States.State4) },
{ '5', new StateAction(IntegralDigit, States.State4) },
{ '6', new StateAction(IntegralDigit, States.State4) },
{ '7', new StateAction(IntegralDigit, States.State4) },
{ '8', new StateAction(IntegralDigit, States.State4) },
{ '9', new StateAction(IntegralDigit, States.State4) },
{ '.', new StateAction(DecimalPoint, States.State5) },
{ '+', new StateAction(OperatorNotAllowed, States.State0) },
{ '-', new StateAction(OperatorNotAllowed, States.State0) },
{ '*', new StateAction(OperatorNotAllowed, States.State0) },
{ '/', new StateAction(OperatorNotAllowed, States.State0) },
{ '=', new StateAction(Result, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining integral part of second operand
state4 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(IntegralDigit, States.State4) },
{ '1', new StateAction(IntegralDigit, States.State4) },
{ '2', new StateAction(IntegralDigit, States.State4) },
{ '3', new StateAction(IntegralDigit, States.State4) },
{ '4', new StateAction(IntegralDigit, States.State4) },
{ '5', new StateAction(IntegralDigit, States.State4) },
{ '6', new StateAction(IntegralDigit, States.State4) },
{ '7', new StateAction(IntegralDigit, States.State4) },
{ '8', new StateAction(IntegralDigit, States.State4) },
{ '9', new StateAction(IntegralDigit, States.State4) },
{ '.', new StateAction(DecimalPoint, States.State5) },
{ '+', new StateAction(CalcAndOperator, States.State3) },
{ '-', new StateAction(CalcAndOperator, States.State3) },
{ '*', new StateAction(CalcAndOperator, States.State3) },
{ '/', new StateAction(CalcAndOperator, States.State3) },
{ '=', new StateAction(CalcAndResult, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
// Defining decimal part of subsequent operand.
state5 = new Dictionary<char, StateAction>
{
{ '0', new StateAction(FractionalDigit, States.State5) },
{ '1', new StateAction(FractionalDigit, States.State5) },
{ '2', new StateAction(FractionalDigit, States.State5) },
{ '3', new StateAction(FractionalDigit, States.State5) },
{ '4', new StateAction(FractionalDigit, States.State5) },
{ '5', new StateAction(FractionalDigit, States.State5) },
{ '6', new StateAction(FractionalDigit, States.State5) },
{ '7', new StateAction(FractionalDigit, States.State5) },
{ '8', new StateAction(FractionalDigit, States.State5) },
{ '9', new StateAction(FractionalDigit, States.State5) },
{ '.', new StateAction(DecimalPointNotAllowed, States.State0) },
{ '+', new StateAction(CalcAndOperator, States.State3) },
{ '-', new StateAction(CalcAndOperator, States.State3) },
{ '*', new StateAction(CalcAndOperator, States.State3) },
{ '/', new StateAction(CalcAndOperator, States.State3) },
{ '=', new StateAction(CalcAndResult, States.State0) },
{ 'C', new StateAction(Clear, States.State0) }
};
OperatorFunctions = new Dictionary<char, Func<double, double, double>> {
{ '+', PlusOperator},
{ '-', MinusOperator },
{ '*', MultiplicationOperator },
{ '/', DivisionOperator } };
stateSet = new Dictionary<States, IDictionary<char, StateAction>>()
{
{States.State0, state0 },
{States.State1, state1 },
{States.State2, state2 },
{States.State3, state3 },
{States.State4, state4 },
{States.State5, state5 }
};
//
ResetCalculator();
}
public double Calculate(char key)
{
stateSet[state][key].Action(key);
state = stateSet[state][key].TransitionToState;
return accumulator;
}
#region Key Functions
private void StartOfNewCalculation(char key)
{
accumulator = 0.0;
state = stateSet[state][key].TransitionToState;
stateSet[state][key].Action(key);
}
private void FirstIntegralDigit(char key)
{
accumulator = accumulator * 10.0 + Char.GetNumericValue(key);
}
private void DecimalPoint(char key)
{
// No action required. Just a change of state
}
private void FirstFractionalDigit(char key)
{
fractionalDivisor *= 10.0;
accumulator = accumulator + (Char.GetNumericValue(key) / fractionalDivisor);
}
private void Operator(char key)
{
ResetNumerics();
operatorInWaiting = key;
}
private void IntegralDigit(char key)
{
currentOperand = currentOperand * 10.0 + Char.GetNumericValue(key);
}
private void FractionalDigit(char key)
{
fractionalDivisor *= 10.0;
currentOperand = currentOperand + (Char.GetNumericValue(key) / fractionalDivisor);
}
private void CalcAndOperator(char key)
{
ExecuteStackedOperator();
Operator(key);
}
private void DecimalPointNotAllowed(char key)
{
ResetCalculator();
throw new Exception("Error: Decimal Point not valid");
}
private void OperatorNotAllowed(char key)
{
ResetCalculator();
throw new Exception("Error: Operator not valid");
}
private void Result(char key)
{
ResetNumerics();
}
private void CalcAndResult(char key)
{
ExecuteStackedOperator();
ResetNumerics();
}
private void Clear(char key)
{
ResetCalculator();
}
#endregion Key Functions
#region Operator Functions
private double PlusOperator(double operand1, double operand2)
{
return operand1 + operand2;
}
private double MinusOperator(double operand1, double operand2)
{
return operand1 - operand2; ;
}
private double MultiplicationOperator(double operand1, double operand2)
{
return operand1 * operand2;
}
private double DivisionOperator(double operand1, double operand2)
{
return operand1 / operand2;
}
#endregion Operator Functions
#region State transition and Operator execution
private void TransitionState(States requiredState)
{
state = requiredState;
}
private void ExecuteStackedOperator()
{
accumulator = OperatorFunctions[operatorInWaiting](accumulator, currentOperand);
}
#endregion State transition and Operator execution
private void ResetCalculator()
{
state = 0;
accumulator = 0.0;
ResetNumerics();
TransitionState(States.State0);
}
private void ResetNumerics()
{
currentOperand = 0.0;
fractionalDivisor = 1.0;
}
}
}
using System;
namespace Calculator.Models
{
public class StateAction
{
public StateAction(Action<char> action, States transitionToState)
{
Action = action;
TransitionToState = transitionToState;
}
public States TransitionToState { get; private set; }
public Action<Char> Action { get; private set; }
}
}
I have put together a complete C#/WPF implementation of the Calculator. There are no ‘if’ statements or switch statements in the implementation. I will admit that there are two null coalesing statements, which can be argued are conditionals. Unfortunately the C# Event functionality (which btw I think is brilliant) does not provide a mechanism to know when an Event has been subscribed to/ unsubscribed from. And so before triggering the Event’s delegates you do have to test if it is null. (ie whether or not it has not been subscribed to).
The complete code is available to download from github at https://github.com/SteveD430/Calculator

Pros & Cons
Before progressing further, I would just like to touch on some of the Pros & Cons of State Oriented programming
Pros to using conditional statements
- They match our thought processes
- If they are not too complex then it is easy to understand what is being tested and what action will be executed if the test is true
- If what is being tested is local then it is easy to determine how the condition will be triggered
Cons to using Conditional Statements
The cons to using conditional statements are really summed up in the caveats attached to the last two pros – If the tests are not too complex and if what is being tested is local. The problem with conditionals is that the condition being tested may not related to the local code. If what is being tested are conditions set-up in another section of code, possibly completely unrelated with code checking the condition, then it can be nigh impossible to understand why the program is in the state that it is. Which means, when something goes wrong, it can be extremely difficult to work out why it went wrong. You can find yourself in that classic situation where the only information is “The Computer – It say No”.
I am sure the following is a scenario we all recognise: Repeatedly, in the debugger, stepping through the same code, using same start conditions, setting up complex watch statements in a vain attempt to track down the chain of events that lead to the object or objects under test being set to the state that caused the problem. And when the problem is finally understood, assuming it ever is, it could well be that it is too complex to resolve, or resolving it at the start of the events too risky, or it may even be a valid scenario that had not previously been considered. Whatever the reason, the solution, all to often, is to “Add in another ‘if’ statement to trap the condition, thereby solving this instance of the problem“. Adding another ‘if’ statement makes the code more complex, less maintainable, more likely to cause problems in the future, and is rarely the correct solution.
State Oriented Programming attempts to reverse the ‘if this then that’ processes. Instead of testing the state of an object (or objects) and then conditionally executing some behaviour, SOP sets the behaviour that is needed at the point where the object or objects move(s) into the required state, The behaviour can then be execute either at the point of state transition (event driven paradigm) or injected into the code where the ‘if’ statement would have been (procedural paradigm).
Pros to SOP
- It makes you think about state and state transitions before coding
- It reduces code complexity by removing ‘if’ and other conditional statements
- It associates the behaviour change with the object state change. The state change and behaviour change are tied together code wise
- It dramatically improves the ability to undertake TDD, because you know all possible states and how to trigger them before any coding has taken place. Plus the testing of the code is easier, because it is easier to ensure all code paths are tested.
Cons to SOP
- Not all applications lend themselves to the SOP approach. For instance it is possible for an object to have a very large or even an infinite number of states (well as near infinite as you can get with a PC) – for example if an objects state changes when a double property hits a certain value. Generally Event driven programs (such as UI based apps) lend themselves nicely to the SOP approach. Algorithmic and Data mining apps far less so.
- Languages do not always have the constructs that make implementing SOP easy. The Calculator example above makes extensive use of pointers to functions, dictionaries, maps, events and delegates. It would be difficult to use an SOP approach without these features.

